对于有 do-算子 的因果效应，用被称为 identification 的方法把它转变为对应的统计估计量之后，因果推断的任务现在变成估计统计估计量，即转变后的因果效应。在深入到任何具体的因果效应估计方法之前，我们简要的介绍因果效应估计的问题设置。
前面 causal_model 中提到每个因果结构都有对应的有向无环图（DAG），又称为因果图。DAG 中每一个子父关系可以用一个确定性函数 $F$来表示。
$$X_i = F_i (pa_i, \eta_i), i = 1, \dots, n$$
其中，$pa_i$ 是 $x_i$ 在 $F$ 中的父节点；$\eta_i$ 是外生的随机干扰，不会在分析中出现。我们称这些函数为结构方程模型（Structural Equation Model，SEM）。
对于满足后门准则（参考 identification）的变量集 $W$，变量 $X$ 对于结果 $Y$ 的因果效应可由以下公式表示：
$$P(y|do(x)) = \sum_w P(y| x, w)P(w).$$
在潜在结果框架中，使上述等式有效的变量 X 也被称为在给定 W 下的"条件可忽略"；满足这个条件的变量组 W 被称为调整集合。在结构化方程模型的语言里，这些关系可表示为：
$$ X= F_1 (W, \epsilon), $$ $$ Y= F_2 (W, X, \eta). $$
我们的问题可以用结构化方程模型表示。
具体来说，YLearn中一个尤其重要的因果量是差
$$\mathbb{E}(Y|do(X=X_1)) - \mathbb{E}(Y|do(X=X_0))$$
也被称为 平均治疗效应(ATE)，其中 $Y$ 被称为 结果 而 $X$ 被称为 治疗 。此外，当条件独立（条件可忽略性）成立时，给定一组变量 $W$ 对结果 $Y$ 和治疗 $X$ 都有潜在的影响，ATE 能够这样估计
$$E(Y|X=x_1, w) - E(Y|X=x_0, w).$$
使用结构化方程模型，我们可以把上述关系描述为
$$X = F_1 (W, \epsilon) $$ $$Y = F_2 (X, W, \eta) $$ $$\text{ATE} = \mathbb{E}\left[ F_2(x_1, W, \eta) - F_2(x_0, W, \eta)\right].$$
假如我们给调整集合 $W$ 的一个子集的变量分配了特殊的角色并把它们命名为 协变量 $V$ ，那么，在结构化方程模型 中， CATE （也被称为 异质治疗效应）被定义为
$$X = F_1 (W, V, \epsilon)$$ $$Y = F_2 (X, W, V, \eta)$$ $$\text{CATE} = \mathbb{E}[F_2(x_1, W, V, \eta) - F_2(x_0, W, V,\eta)| V =v].$$
除了是效应的差的因果估计量，还有一个因果量 反事实 。对于这个量，我们估计如下的因果估计量：
$$\mathbb{E} [Y|do(x), V=v].$$
许多的估计器模型需要通常无法测试的无混淆条件。一个适用的方法是，在深入具体的估计之前，构建我们的因果效应的上下界。
YLearn中有四个不同的界。我们在下面简单介绍它们。细节请参考 Neal2020 。
无假设界
假设
$$ \forall x, a \leq Y(do(x)) \leq b,$$
那么我们有
$$ \mathbb{E}[Y(do(1)) - Y(do(0))] \leq \pi \mathbb{E}[Y|X = 1] + (1 - \pi) b - \pi a - (1 - \pi )\mathbb{E}[Y| X = 0] $$ $$ \mathbb{E}[Y(do(1)) - Y(do(0))] \geq \pi \mathbb{E}[Y|X = 1] + (1 - \pi) a - \pi b - (1 - \pi )\mathbb{E}[Y| X = 0] $$
其中 $\pi$ 是令 $X=1$ 的概率。
非负单调治疗响应界
假如
$$ \forall i, Y(do(1)) \geq Y(do(0)),$$
其意味着 治疗只会帮助 。那么我们有下面的界：
$$ \mathbb{E}[Y(do(1)) - Y(do(0))] \leq \pi \mathbb{E}[Y|X = 1] + (1 - \pi) b - \pi a - (1 - \pi )\mathbb{E}[Y| X = 0]$$ $$\mathbb{E}[Y(do(1)) - Y(do(0))] \geq 0$$
非正单调治疗响应界
假如
$$ \forall i, Y(do(1)) \leq Y(do(0)),$$
其意味着 治疗不会帮助 。那么我们有下面的界：
$$ \mathbb{E}[Y(do(1)) - Y(do(0))] \leq 0$$ $$\mathbb{E}[Y(do(1)) - Y(do(0))] \geq \pi \mathbb{E}[Y|X = 1] + (1 - \pi) a - \pi b - (1 - \pi )\mathbb{E}[Y| X = 0].$$
最优治疗选择界
假如
$$ X = 1 \implies Y(do(1)) \geq Y(do(0)) $$ $$ X = 0 \implies Y(do(0)) \geq Y(do(1)) $$
其意味着 人们总是接受对他们而言最好的治疗 。那么我们有下面的界：
$$ \mathbb{E}[Y(do(1)) - Y(do(0))] \leq \pi \mathbb{E}[Y|X = 1] - \pi a$$ $$ \mathbb{E}[Y(do(1)) - Y(do(0))] \geq (1 - \pi) a - (1 - \pi )\mathbb{E}[Y| X = 0].$$
还有一种最优治疗选择界：
$$ \mathbb{E}[Y(do(1)) - Y(do(0))] \leq \mathbb{E}[Y|X = 1] - \pi a - (1 - \pi)\mathbb{E}[Y|X=0] $$ $$ \mathbb{E}[Y(do(1)) - Y(do(0))] \geq \pi\mathbb{E}[Y|X = 1] + (1 - \pi) a - \mathbb{E}[Y| X = 0].$$
import numpy as np
from ylearn.estimator_model.approximation_bound import ApproxBound
from ylearn.exp_dataset.exp_data import meaningless_discrete_dataset_
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
data = meaningless_discrete_dataset_(num=num, confounder_n=3, treatment_effct=[2, 5, -8], random_seed=0)
treatment = 'treatment'
w = ['w_0', 'w_1', 'w_2']
outcome = 'outcome'
bound = ApproxBound(y_model=RandomForestRegressor(), x_model=RandomForestClassifier())
bound.fit(data=data, treatment=treatment, outcome=outcome, covariate=w,)
>>> ApproxBound(y_model=RandomForestRegressor(),
x_prob=array([[0. , 0.99, 0.01],
[0. , 0.99, 0.01],
[1. , 0. , 0. ],
...,
[0. , 1. , 0. ],
[0.01, 0.99, 0. ],
[0.01, 0.99, 0. ]]),
x_model=RandomForestClassifier())
b_l, b_u = bound.estimate()
b_l.mean()
>>> -7.126728994957785
b_u.mean()
>>> 8.994011617037696
元学习器是一种估计模型，旨在当处理手段为离散变量时通过机器学习模型去评估CATE。治疗方案为离散变量的意思也就是当无混淆条件下非1即0。通常来讲，它利用多个可灵活选择的机器学习模型。
YLearn 实现了3个元学习器: S-Learner, T-Learner, and X-Learner.
S-Learner
SLearner 采用一个机器学习模型来评估因果效应。具体来说，我们用机器学习模型 $f$ 从治疗方案 $x$ 和调整集 (或者协变量) $w$ 中拟合一个模型去预测结果 $y$:
$$ y = f(x, w).$$
因果效应 $\tau(w)$ 被计算为:
$$ \tau(w) = f(x=1, w) - f(x=0, w).$$
T-Learner
TLearner的问题是当调整集向量为多维时治疗方案向量仅为一维。因此，如果调整集的维度超过1，那么评估结果将总是逼近于0。 TLearner用两个机器学习模型去评估因果效应。具体来讲，令 $w$ 为调整集（或协变量），我们
$$ y_t = f_t(w)$$
其中, $x=$ treat.
$$ y_0 = f_0(w)$$
其中, $x=$ control.
计算因果效应 $\tau(w)$ 作为两个模型预测结果的差异:
$$ \tau(w) = f_t(w) - f_0(w).$$
X-Learner
TLearner未能完全有效地利用数据，XLearner可以解决这个问题。训练一个XLearner可以分为3步:
与TLearner类似, 我们首先分别训练两个不同的模型对于控制组和治疗组:
$$ f_0(w) \text{for the control group} $$ $$ f_1(w) \text{for the treat group}.$$
生成两个新数据集 ${(h_0, w)}$ 用控制组, ${(h_1, w)}$用治疗组。 其中
$$ h_0 = f_1(w) - y_0,$$ $$ h_1 = y_1 - f_0(w). $$
然后，训练两个机器学习模型在这些数据集中 $k_0(w)$ 和 $k_1(w)$
$$ h_0 = k_0(w) $$ $$ h_1 = k_1(w).$$
结合以上两个模型得到最终的模型:
$$ g(w) = k_0(w)a(w) + k_1(w)(1 - a(w))$$
其中, $a(w)$ 是一个调整 $k_0$ 和 $k_1$ 的权重调整系数。
最后, 因果效应 $\tau(w)$ 通过以下方式评估:
$$ \tau(w) = g(w).$$
import numpy as np
from numpy.random import multivariate_normal
from sklearn.ensemble import RandomForestClassifier, GradientBoostingRegressor
import matplotlib.pyplot as plt
from ylearn.estimator_model.meta_learner import SLearner, TLearner, XLearner
from ylearn.estimator_model.doubly_robust import DoublyRobust
from ylearn.exp_dataset.exp_data import binary_data
from ylearn.utils import to_df
# build the dataset
d = 5
n = 2500
n_test = 250
y, x, w = binary_data(n=n, d=d, n_test=n_test)
data = to_df(outcome=y, treatment=x, w=w)
outcome = 'outcome'
treatment = 'treatment'
adjustment = data.columns[2:]
# build the test dataset
treatment_effect = lambda x: (1 if x[1] > 0.1 else 0) * 8
w_test = multivariate_normal(np.zeros(d), np.diag(np.ones(d)), n_test)
delta = 6/n_test
w_test[:, 1] = np.arange(-3, 3, delta)
SLearner
s = SLearner(model=GradientBoostingRegressor())
s.fit(data=data, outcome=outcome, treatment=treatment, adjustment=adjustment) # training
s_pred = s.estimate(data=test_data, quantity=None) # predicting
TLearner
t = TLearner(model=GradientBoostingRegressor())
t.fit(data=data, outcome=outcome, treatment=treatment, adjustment=adjustment) # training
t_pred = t.estimate(data=test_data, quantity=None) # predicting
XLearner
x = XLearner(model=GradientBoostingRegressor())
x.fit(data=data, outcome=outcome, treatment=treatment, adjustment=adjustment) # training
x_pred = x.estimate(data=test_data, quantity=None) # predicting
我们使用大写字母表示矩阵，小写字母表示向量。治疗由 $x$ 表示，结果由 $y$ 表示，协变量由 $v$ 表示，且其他的调整集合变量是 $w$。 希腊字母用于错误项。
双机器学习（DML）模型 Chern2016 适用于当治疗，结果，变量的同时影响治疗和结果的所有的混杂因素都被观察到。令 $y$ 为结果，$x$ 为治疗，一个DML模型解决如下的因果效应估计（CATE估计）：
$$ y = F(v) x + g(v, w) + \epsilon $$ $$ x = h(v, w) + \eta$$
其中 $F(v)$ 是CATE以 $v$ 为条件。 此外，为了估计 $F(v)$，我们注意到
$$ y - \mathbb{E}[y|w, v] = F(v) (x - \mathbb{E}[x|w, v]) + \epsilon. $$
因此通过首先估计 $\mathbb{E}[y|w, v]$ 和 $\mathbb{E}[x|w,v]$ 为
$$ m(v, w) = \mathbb{E}[y|w, v] $$ $$ h(v, w) = \mathbb{E}[x|w,v],$$
我们能够得到一个新的数据集： $(\tilde{y}, \tilde{x})$ 其中
$$ \tilde{y} = y - m(v, w) $$ $$ \tilde{x} = x - h(v, w)$$
这样 $\tilde{y}$ 和 $\tilde{x}$ 之间的关系是线性的
$$ \tilde{y} = F(v) \tilde{x} + \epsilon$$
其能够被线性回归模型简单的建模。
另一方面，在现在的版本， $F(v)$ 采取形式
$$ F_{ij}(v) = \sum_k H_{ijk} \rho_k(v).$$
其中 $H$ 能够被看作一个秩为3的张量且 $\rho_k$ 是协变量 $v$ 的函数，比如，最简单的情况 $\rho(v) = v$ 。因此， $y$ 现在能够被表示为
$$ y_i = \sum_j F_{ij}x_j + g(v, w)_j + \epsilon $$ $$ = \sum_j \sum_k H_{ijk}\rho_k(v)x_j + g(v, w)_j + \epsilon $$
在这个意义上，$\tilde{y}$ 和 $\tilde{x}$ 之间的线性回归问题现在成为，
$$ \tilde{y}_i = \sum_j \sum_k H_{ijk}\rho_k(v) \tilde{x}_j + \epsilon.$$
在YLearn中，我们实现了一个双机器学习模型如 Chern2016 中描述的算法：
令 k (cf_folds in our class) 为一个int. 形成一个k-折随机划分{…, (train_data_i, test_data_i), …,(train_data_k, test_data_k)}。
对于每个i，训练y_model和x_model在train_data_i上，接着评估它们的性能在test_data_i中，其结果会被保存为 $(\hat{y}_k, \hat{x}_k)$ 。 所有的 $(\hat{y}_k, \hat{x}_k)$ 将会合并以提供新的数据集 $(\hat{y}, \hat{x})$ 。
定义差
$$ \tilde{y} = y - \hat{y}, $$ $$ \tilde{x}= (x - \hat{x}) \otimes v.$$
接着形成新的数据集 $(\tilde{y}, \tilde{x})$.
$$ f \cdot v.$$
from sklearn.ensemble import RandomForestRegressor
from ylearn.exp_dataset.exp_data import single_continuous_treatment
from ylearn.estimator_model.double_ml import DoubleML
# build the dataset
train, val, treatment_effect = single_continuous_treatment()
adjustment = train.columns[:-4]
covariate = 'c_0'
outcome = 'outcome'
treatment = 'treatment'
dml = DoubleML(x_model=RandomForestRegressor(), y_model=RandomForestRegressor(), cf_fold=3,)
dml.fit(train, outcome, treatment, adjustment, covariate,)
>>> 06-23 14:02:36 I ylearn.e.double_ml.py 684 - _fit_1st_stage: fitting x_model RandomForestRegressor
>>> 06-23 14:02:39 I ylearn.e.double_ml.py 690 - _fit_1st_stage: fitting y_model RandomForestRegressor
>>> DoubleML(x_model=RandomForestRegressor(), y_model=RandomForestRegressor(), yx_model=LinearRegression(), cf_fold=3)
双鲁棒方法（参考 Funk2010 ）估计因果效应当治疗是离散的且满足无混淆条件。训练一个双鲁棒模型由3步组成。
令 $k$ 为一个int。形成一个对数据 ${(X_i, W_i, V_i, Y_i)}_{i = 1}^n$ 的 $K$-fold 随机划分，这样
$$ {(x_i, w_i, v_i, y_i)}_{i = 1}^n = D_k \cup T_k$$
其中 $D_k$ 表示训练数据且 $T_k$ 表示测试数据且 $\cup_{k = 1}^K T_k = {(X_i, W_i, V_i, Y_i)}_{i = 1}^n$.
对于每个 $k$, 训练两个模型 $f(X, W, V)$ 和 $g(W, V)$ 在 $D_k$ 上来分别预测 $y$ 和 $x$。接着估计它们在 $T_k$ 中的性能， 结果保存为 ${(\hat{X}, \hat{Y})}_k$ 。所有的 ${(\hat{X}, \hat{Y})}_k$ 将被合并来给出新的数据集 ${(\hat{X}_i, \hat{Y}i(X, W, V))}{i = 1}^n$ 。
对于任何给定的一对治疗组其中 $X=x$ 和控制组其中 $X = x_0$ ，我们构建最终数据集 ${(V, \tilde{Y}_x - \tilde{Y}_0)}$ 其中 $\tilde{Y}_x$ 被定义为
$$ \tilde{Y}_x = \hat{Y}(X=x, W, V) + \frac{(Y - \hat{Y}(X=x, W, V)) * \mathbb{I}(X=x)}{P[X=x| W, V]} $$ $$ \tilde{Y}_0 = \hat{Y}(X=x_0, W, V) + \frac{(Y - \hat{Y}(X=x_0, W, V)) * \mathbb{I}(X=x_0)}{P[X=x_0| W, V]} $$
并在这个数据集上训练最终的机器学习模型 $h(W, V)$ 来预测因果效应 $\tau(V)$
$$ \tau(V) = \tilde{Y}_x - \tilde{Y}_0 = h(V).$$
接着我们可以直接估计因果效应，通过传入协变量 $V$ 到模型 $h(V)$ 。
import numpy as np
from numpy.random import multivariate_normal
from sklearn.ensemble import RandomForestClassifier, GradientBoostingRegressor
import matplotlib.pyplot as plt
from ylearn.estimator_model.meta_learner import SLearner, TLearner, XLearner
from ylearn.estimator_model.doubly_robust import DoublyRobust
from ylearn.exp_dataset.exp_data import binary_data
from ylearn.utils import to_df
# build the dataset
d = 5
n = 2500
n_test = 250
y, x, w = binary_data(n=n, d=d, n_test=n_test)
data = to_df(outcome=y, treatment=x, w=w)
outcome = 'outcome'
treatment = 'treatment'
adjustment = data.columns[2:]
# build the test dataset
treatment_effect = lambda x: (1 if x[1] > 0.1 else 0) * 8
w_test = multivariate_normal(np.zeros(d), np.diag(np.ones(d)), n_test)
delta = 6/n_test
w_test[:, 1] = np.arange(-3, 3, delta)
训练 DoublyRobust 模型。
dr = DoublyRobust(
x_model=RandomForestClassifier(n_estimators=100, max_depth=100, min_samples_leaf=int(n/100)),
y_model=GradientBoostingRegressor(n_estimators=100, max_depth=100, min_samples_leaf=int(n/100)),
yx_model=GradientBoostingRegressor(n_estimators=100, max_depth=100, min_samples_leaf=int(n/100)),
cf_fold=1,
random_state=2022,
)
dr.fit(data=data, outcome=outcome, treatment=treatment, covariate=adjustment,)
dr_pred = dr.estimate(data=test_data, quantity=None).squeeze()
因果树是一个数据驱动的方法，用来把数据划分为因果效应幅度不同的亚群 Athey2015。这个方法在给定调整集（协变量） $V$ 无混淆满足时适用。 感兴趣的因果效应是CATE：
$$ \tau(v) := \mathbb{}[Y_i(do(X=x_t)) - Y_i(do(X=x_0)) | V_i = v] $$
因为事实上反事实无法被观测到， Athey2015 开发了一个诚实的方法，其中损失函数（构建树的准则）被设计为
$$ e (S_{tr}, \Pi) := \frac{1}{N_{tr}} \sum_{i \in S_{tr}} \hat{\tau}^2 (V_i; S_{tr}, \Pi) - \frac{2}{N_{tr}} \cdot \sum_{\ell \in \Pi} \left( \frac{\Sigma^2_{S_{tr}^{treat}}(\ell)}{p} + \frac{\Sigma^2_{S_{tr}^{control}}(\ell)}{1 - p}\right) $$
其中 $N_{tr}$ 是训练集 $S_{tr}$ 中样本的数量, $p$ 是训练集中治疗组和控制组样本个数的比，且
$$ \hat{\tau}(v)=\frac{1}{num({i\in S_{treat}: V_i \in \ell(v; \Pi)})}\sum_{ {i\in S_{treat}: V_i \in \ell(v; \Pi)}} Y_i $$ $$ - \frac{1}{num({i\in S_{control}: V_i \in \ell(v; \Pi)})} \sum_{ {i\in S_{control}: V_i \in \ell(v; \Pi)}} Y_i. $$
import numpy as np
import matplotlib.pyplot as plt
from ylearn.estimator_model.causal_tree import CausalTree
from ylearn.exp_dataset.exp_data import sq_data
from ylearn.utils._common import to_df
# build dataset
n = 2000
d = 10
n_x = 1
y, x, v = sq_data(n, d, n_x)
true_te = lambda X: np.hstack([X[:, [0]]**2 + 1, np.ones((X.shape[0], n_x - 1))])
data = to_df(treatment=x, outcome=y, v=v)
outcome = 'outcome'
treatment = 'treatment'
adjustment = data.columns[2:]
# build test data
v_test = v[:min(100, n)].copy()
v_test[:, 0] = np.linspace(np.percentile(v[:, 0], 1), np.percentile(v[:, 0], 99), min(100, n))
test_data = to_df(v=v_test)
训练 CausalTree 并在测试数据中使用它：
ct = CausalTree(min_samples_leaf=3, max_depth=5)
ct.fit(data=data, outcome=outcome, treatment=treatment, adjustment=adjustment)
ct_pred = ct.estimate(data=test_data)
工具变量（IV）处理的情况是：当存在未观察到的混淆变量，且其同时影响治疗 $X$ 和结果 $Y$ 时，需要进行因果效应估计。定义：对于任何在 $Z$ 中的变量 $z$，如果满足下面条件，我们称变量集合 $Z$ 为 工具变量（IV）：
在这样的情况下，我们必须首先找到IV（其可以通过使用 CausalModel 完成，参考 identification ）。举个例子，变量 $Z$ 在下面的图中
可以作为一个合理的IV，在存在未观察到的混淆变量 $U$ 时估计 $X$ 对 $Y$ 的因果效应。
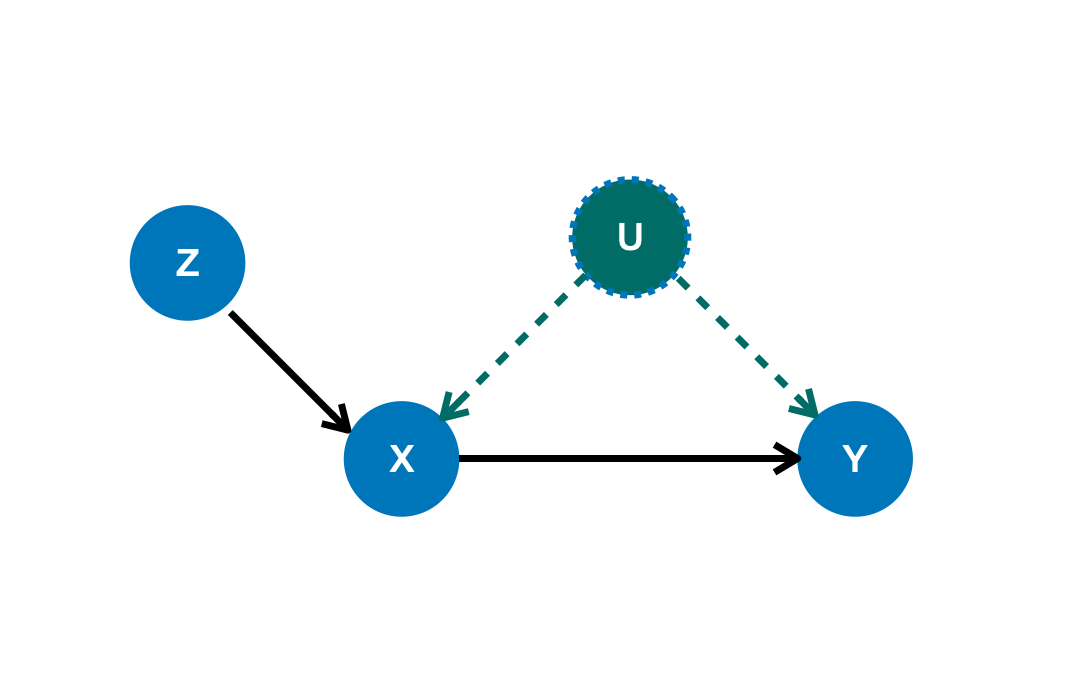
YLearn关于IV实现两个不同的方法：deepiv Hartford ，对IV使用深度学习模型和IV的无参数模型 Newey2002。
IV框架的目的是预测结果 $y$ 的值当治疗 $x$ 给定时。除此之外，还存在一些协变量向量 $v$ 其同时影响 $y$ 和 $x$。 还有一些未观察到的混淆因素 $e$ 其潜在影响 $y$ ，$x$ 和 $v$ 。因果问题的核心部分是估计因果量。
$$ \mathbb{E}[y| do(x)] $$
下面的因果图，其中因果关系的集合由函数的集合决定
$$ y = f(x, v) + e $$ $$ x = h(v, z) + \eta$$ $$ \mathbb{E}[e] = 0. $$
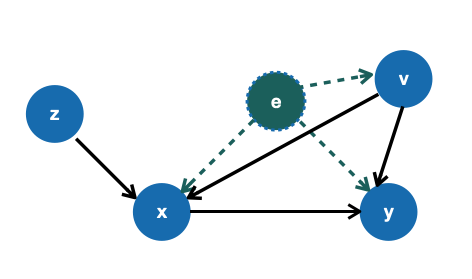
IV框架通过做两步估计解决这个问题：
估计 $\hat{H}(z, v)$ 其捕获在 $x$ 和变量 $(z, v)$ 之间的关系。
用预测的结果 $\hat{H}(z, v)$ 取代 $x$ 给定 $(v, z)$ 。接着估计 $\hat{G}(x, v)$ 来构建 $y$ 和 $(x, v)$ 之间的关系。
最终的因果效应能够被计算。
用于估计因果效应的估计器模型不能被简单的评价，因为事实上真实的效应不能被直接观察到。这和平常的，结果可以用比如说损失函数的值简单评价的机器学习任务不同。
Schuler 的作者提出了一个框架，一个由 Nie 表明的模式，来评估不同的估计器模型估计的因果效应。粗略的说，这个框架是双机器学习方法的直接应用。
具体的说，对于一个因果效应模型ce_model （在训练集上训练好的），等待被评价，我们
在通常和训练集不同的验证集中，训练一个模型 y_model 来估计结果 $y$ 和一个 x_model 来估计治疗 $x$ ；
在验证集 $D_{val}$ 中，令 $\tilde{y}$ 和 $\tilde{x}$ 表示差
$$ \tilde{y} = y - \hat{y}(v), $$ $$ \tilde{x} = x - \hat{x}(v) $$
其中 $\hat{y}$ 和 $\hat{x}$ 是在 $D_{val}$ 中估计的结果和治疗基于协变量 $v$ 。 此外，令
$$ \tau(v)$$
表明在 $D_{val}$ 中由 ce_model 估计的因果效应，那么对于ce_model因果效应的度量标准这样计算。
$$ E_{V}[(\tilde{y} - \tilde{x} \tau(v))^2].$$
from sklearn.ensemble import RandomForestRegressor
from ylearn.exp_dataset.exp_data import single_binary_treatment
from ylearn.estimator_model.meta_learner import TLearner
train, val, te = single_binary_treatment()
rloss = RLoss(
x_model=RandomForestClassifier(),
y_model=RandomForestRegressor(),
cf_fold=1,
is_discrete_treatment=True
)
rloss.fit(
data=val,
outcome=outcome,
treatment=treatment,
adjustment=adjustment,
covariate=covariate,
)
est = TLearner(model=RandomForestRegressor())
est.fit(
data=train,
treatment=treatment,
outcome=outcome,
adjustment=adjustment,
covariate=covariate,
)
rloss.score(est)
>>> 0.20451977
YLearn实现了上述的多个估计器模型，可用于不同的，如ATE： $$\mathbb{E}[F_2(x_1, W, \eta) - F_2(x_0, W, \eta)]$$
及CATE： $$\mathbb{E}[F_2(x_1, W, V, \eta) - F_2(x_0, W, V, \eta)]$$
的估计任务。YLearn中概念EstimatorModel 就是为这个目的设计的 。一个常见的 EstimatorModel 应该有如下结构：
class BaseEstModel:
"""
Base class for various estimator model.
Parameters
----------
random_state : int, default=2022
is_discrete_treatment : bool, default=False
Set this to True if the treatment is discrete.
is_discrete_outcome : bool, default=False
Set this to True if the outcome is discrete.
categories : str, optional, default='auto'
"""
def fit(
self,
data,
outcome,
treatment,
**kwargs,
):
"""Fit the estimator model.
Parameters
----------
data : pandas.DataFrame
The dataset used for training the model
outcome : str or list of str, optional
Names of the outcome variables
treatment : str or list of str
Names of the treatment variables
Returns
-------
instance of BaseEstModel
The fitted estimator model.
"""
def estimate(
self,
data=None,
quantity=None,
**kwargs
):
"""Estimate the causal effect.
Parameters
----------
data : pd.DataFrame, optional
The test data for the estimator to evaluate the causal effect, note
that the estimator directly evaluate all quantities in the training
data if data is None, by default None
quantity : str, optional
The possible values of quantity include:
'CATE' : the estimator will evaluate the CATE;
'ATE' : the estimator will evaluate the ATE;
None : the estimator will evaluate the ITE or CITE, by default None
Returns
-------
ndarray
The estimated causal effect with the type of the quantity.
"""
def effect_nji(self, data=None, *args, **kwargs):
"""Return causal effects for all possible values of treatments.
Parameters
----------
data : pd.DataFrame, optional
The test data for the estimator to evaluate the causal effect, note
that the estimator directly evaluate all quantities in the training
data if data is None, by default None
"""
可以在以下过程中应用任何 EstimatorModel
对于 pandas.DataFrame 形式的数据，找到治疗、结果、调整集合和协变量的名字。
把数据和治疗、结果、调整集合、协变量的名字传入 EstimatorModel 的 fit() 方法并调用它。
调用 estimate() 方法在测试数据上使用拟合的 EstimatorModel。
